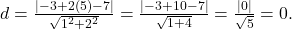A ➡️ distância entre um 🔹 ponto e uma ⬆️ reta é um conceito 📊 fundamental em 🗺️ geometria, com 🚀 aplicações em diversas 🛠️ áreas, como 🎨 engenharia, 🔧 computação gráfica e ⚡️ física. Este 📚 artigo explora o 🔍 conceito, apresenta suas ✨ propriedades, 🎓 exemplos didáticos e 💰 exercícios com ✍️ soluções em formato
Conceito
A distância entre um ponto e uma reta é definida como o comprimento do segmento de reta perpendicular à reta em questão que passa pelo ponto. Geometricamente, essa é a menor distância entre o ponto e qualquer outro ponto pertencente à reta.
Fórmula Geral
Seja uma reta definida pela equação geral:
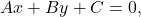
e um ponto  A distância
A distância 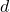 entre o ponto e a reta é dada por:
entre o ponto e a reta é dada por:
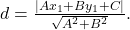
Propriedades
- Perpendicularidade: O segmento que representa a menor distância entre o ponto e a reta é sempre perpendicular à reta.
- Invariância da Distância: A distância é um valor absoluto, ou seja, sempre positiva, mesmo que o ponto esteja “acima” ou “abaixo” da reta.
- Generalidade: A fórmula funciona para retas inclinadas, horizontais e verticais.
Exemplos:
Exemplo 1: Distância de um ponto a uma reta inclinada
Seja a reta 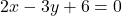 e o ponto
e o ponto 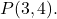
Solução: Aplicando a fórmula:
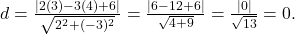
Neste caso, 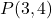 está sobre a reta.
está sobre a reta.
Exemplo 2: Distância de um ponto a uma reta horizontal
Seja a reta 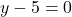 e o ponto
e o ponto 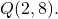
Solução: Aqui, temos  ,
,  e
e 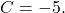
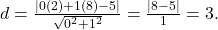
A distância é 3 unidades.
Exemplo 3: Distância de um ponto a uma reta vertical
Seja a reta  e o ponto
e o ponto 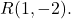
Solução: Aqui,  ,
, 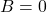 e
e 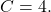
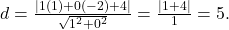
A distância é 5 unidades.
Exercícios
- Calcule a distância entre o ponto
 e a reta
e a reta 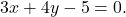 Resposta:
Resposta: 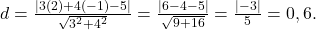
- Determine a distância do ponto
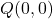 à reta
à reta 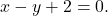 Resposta:
Resposta: 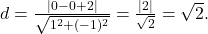
- Encontre a distância entre o ponto
 e a reta
e a reta  Resposta:
Resposta: