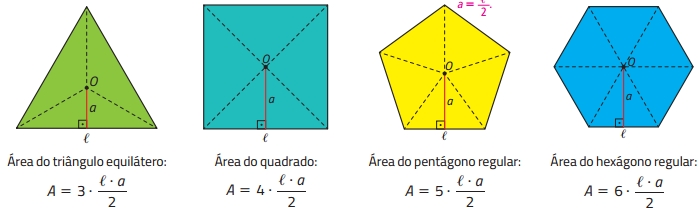
**Área de um Polígono Regular: Propriedades, Exemplos e Exercícios**

Os polígonos regulares são figuras geométricas com lados e ângulos internos iguais. Esses polígonos possuem aplicações na geometria, arquitetura, design e em várias áreas do conhecimento. Vamos explorar suas propriedades, aprender a calcular a área de um polígono regular e resolver exemplos práticos para consolidar o aprendizado.

—

### **Propriedades de um Polígono Regular**

1. **Lados iguais:** Todos os lados possuem o mesmo comprimento.
2. **Ângulos iguais:** Todos os ângulos internos têm a mesma medida.
3. **Centro e raio:** O polígono regular pode ser circunscrito em um círculo. O raio do círculo é chamado de **raio do polígono**.
4. **Apótema:** A apótema é o segmento que liga o centro do polígono ao ponto médio de um dos seus lados, sendo perpendicular a ele. A apótema é fundamental para o cálculo da área.

### **Fórmula da Área de um Polígono Regular**

A área de um polígono regular pode ser calculada pela fórmula:

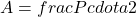
Onde:
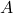– é a área do polígono.
– é o perímetro do polígono (soma de todos os lados).
– é a apótema.

Outra fórmula alternativa, considerando o número de lados () e o comprimento de cada lado (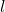), é:

—

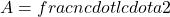
### **Exemplo 1: Triângulo Equilátero**

Calcule a área de um triângulo equilátero com lado de 6 cm.

1. **Identificar o perímetro e a apótema:**
– Perímetro: .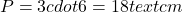
– Apótema: Para o triângulo equilátero, a apótema é . Logo, .

2. **Aplicar a fórmula:**
.

—

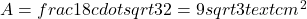### **Exemplo 2: Hexágono Regular**

Calcule a área de um hexágono regular com lado de 4 cm.

1. **Identificar o perímetro e a apótema:**
– Perímetro: .
– Apótema: Para o hexágono regular, a apótema é . Logo, .

2. **Aplicar a fórmula:**
.

—

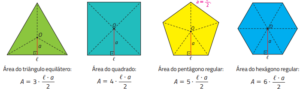
### **Representações Gráficas**

#### Triângulo Equilátero
(Desenho do triângulo com apótema e centro destacados.)

#### Hexágono Regular
(Desenho do hexágono com apótema e raio marcados.)

—

### **Exercícios Propostos**

1. Calcule a área de um quadrado regular com lado de 5 cm.

**Resposta:**

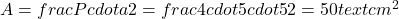
2. Um pentágono regular tem lado de 10 cm e apótema de 13,8 cm. Calcule sua área.

**Resposta:**

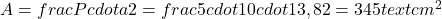
3. Determine a área de um octógono regular com lado de 8 cm e apótema de 9,7 cm.

**Resposta:**

—

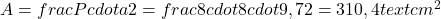
Explore o uso dessas fórmulas e resolva os exercícios para dominar o cálculo de áreas em polígonos regulares!