Introdução

O cálculo da área do triângulo é uma habilidade essencial em matemática, com aplicações que vão desde o design arquitetônico até o cálculo de terrenos. Mas você já parou para pensar em como essa fórmula simples pode ser tão versátil e fascinante? Vamos mergulhar nesse universo, desvendando conceitos, fórmulas e aplicações práticas.

---

O que é a Área de um Triângulo?

A área de um triângulo é a medida da superfície interna dessa figura geométrica. Em outras palavras, é o espaço bidimensional que ele ocupa no plano.

Por que calcular a área é importante?

• Construção civil: Determinar o espaço necessário para fundações.
• Agricultura: Medir terrenos com formatos irregulares.
• Design gráfico: Criar elementos proporcionais em projetos visuais.

---

Elementos do Triângulo

Para entender melhor o cálculo da área, é essencial conhecer os elementos básicos de um triângulo:

1. Base

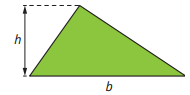
A base é qualquer um dos lados do triângulo que serve como referência para calcular a altura.

2. Altura

A altura é a distância perpendicular entre a base escolhida e o vértice oposto.

3. Tipos de Triângulos

• Equilátero: Todos os lados iguais.
• Isósceles: Dois lados iguais.
• Escaleno: Todos os lados diferentes.
• Retângulo: Possui um ângulo de 90°.

---

Fórmula Clássica da Área

A fórmula mais conhecida para calcular a área de um triângulo é:

Área = (base × altura) ÷ 2

Exemplo Prático

Imagine um triângulo com base de 10 cm e altura de 6 cm. A área será:
Área = (10 × 6) ÷ 2 = 30 cm²

---

Outras Fórmulas para a Área

Além da fórmula clássica, existem métodos alternativos para calcular a área, dependendo das informações disponíveis.

1. Fórmula de Heron

Quando os comprimentos dos três lados são conhecidos, usamos:

Área = √[s(s-a)(s-b)(s-c)]

Onde:

• a, b, c são os lados do triângulo.
• s é o semiperímetro:
  s = (a + b + c) ÷ 2

Exemplo

Um triângulo com lados de 7 cm, 8 cm e 9 cm:
s = (7 + 8 + 9) ÷ 2 = 12
Área = √[12(12-7)(12-8)(12-9)] = √[12 × 5 × 4 × 3] = √720 ≈ 26,83 cm²

---

2. Triângulos Retângulos

Para triângulos retângulos, a base e a altura são simplesmente os dois catetos.

Exemplo

Com catetos de 5 cm e 12 cm:
Área = (5 × 12) ÷ 2 = 30 cm²

3. Fórmula com Seno

Se conhecemos dois lados e o ângulo entre eles:
Área = (a × b × sen(θ)) ÷ 2

Exemplo

Para lados de 8 cm, 10 cm e um ângulo de 60°:
Área = (8 × 10 × sen(60)) ÷ 2 = (80 × 0,866) ÷ 2 ≈ 34,64 cm²

---

Casos Especiais

Triângulos em Coordenadas

Se os vértices do triângulo são conhecidos em um plano cartesiano:
Área = |x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)| ÷ 2

---

Aplicações Práticas

• Engenharia: Dimensionar peças estruturais.
• Geografia: Medir áreas de reservas naturais.
• Arte: Criar composições geométricas equilibradas.

Dicas e Truques

• Sempre escolha a base e a altura mais convenientes para simplificar o cálculo.
• Lembre-se de usar unidades consistentes (cm, m, km, etc.).
• Em triângulos complexos, divida a figura em triângulos menores.

Conclusão

Compreender como calcular a área de um triângulo é mais do que uma habilidade matemática – é uma ferramenta prática para resolver problemas do dia a dia. Seja no trabalho ou nos estudos, dominar esses conceitos abrirá novas possibilidades para você!