A fração geratriz é uma forma de representar uma dízima periódica como uma fração. Isso é útil porque facilita operações matemáticas, como soma, subtração, multiplicação e divisão, que podem ser mais complicadas quando trabalhamos diretamente com números decimais infinitos .

Neste artigo, vamos explorar o passo a passo para encontrar a fração geratriz de uma dízima periódica, além de resolver 5 exercícios práticos.

---

Passo a Passo para Encontrar a Fração Geratriz

Dízima Periódica Simples

1. Escreva a dízima periódica igualada a $x$:
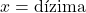
2. Multiplique ambos os lados por 10n, onde $n$ é o número de algarismos no período da dízima: O período é o conjunto de algarismos que se repete. Por exemplo, na dízima $0,333\dots$, o período é “3”.

   

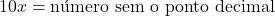
3. Subtraia a equação inicial ($x$) da nova equação ($10x$): Isso elimina a parte infinita e permite isolar $x$.
4. Resolva a equação para encontrar $x$: Simplifique a fração resultante, se necessário.

---

Exemplo Prático: $0,333\dots$

1. Igualamos a dízima a $x$:
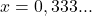
2. Multiplicamos por 10 (pois o período tem 1 algarismo):
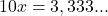
3. Subtraímos as duas equações:
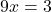
4. Resolvemos para $x$:

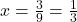
Portanto, a fração geratriz de $0,333\dots$ é 31​.

---

Exercícios Resolvidos

Exercício 1: $0,666\dots$

1. Igualamos a dízima a $x$:
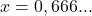
2. Multiplicamos por 10:
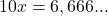
3. Subtraímos as equações:
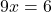
4. Resolvemos para $x$:

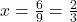
Resposta: A fração geratriz é 32​.

---

Exercício 2: $0,121212\dots$

1. Igualamos a dízima a $x$:
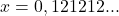
2. Multiplicamos por 100 (pois o período tem 2 algarismos):
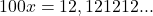
3. Subtraímos as equações:
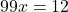
4. Resolvemos para $x$:

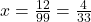
Resposta: A fração geratriz é 334​.

---

Exercício 3: $2,555\dots$

1. Separamos a parte inteira da parte decimal:
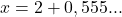
2. Trabalhamos apenas com a parte decimal ($0,555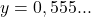\dots$): Multiplicamos por 10: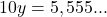
3. Subtraímos as equações:
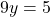
4. Resolvemos para $y$:
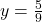
5. Somamos a parte inteira:

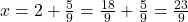
Resposta: A fração geratriz é 923​.

---

Exercício 4: $0,272727\dots$

1. Igualamos a dízima a $x$:
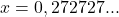
2. Multiplicamos por 100 (pois o período tem 2 algarismos):
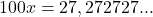
3. Subtraímos as equações:
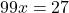
4. Resolvemos para $x$:

Resposta: A fração geratriz é 113​.

---

Exercício 5: $1,484848\dots$

1. Separamos a parte inteira da parte decimal:
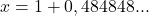
2. Trabalhamos apenas com a parte decimal ($0,484848\dots$): Multiplicamos por 100:
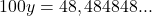
3. Subtraímos as equações:
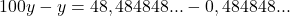
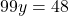
4. Resolvemos para $y$:
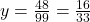
5. Somamos a parte inteira:

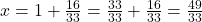
Resposta: A fração geratriz é 3349​.

---

Conclusão

A fração geratriz é uma ferramenta poderosa para simplificar cálculos envolvendo dízimas periódicas. Com o método passo a passo apresentado aqui, você pode transformar qualquer dízima periódica em uma fração de forma clara e sistemática
Os exercícios resolvidos mostram como aplicar esse método na prática, usando notação matemática simples e direta.