# Função Quadrática
A função quadrática é uma das funções mais importantes da matemática, especialmente no estudo da álgebra e do cálculo. Sua forma geral é dada por:
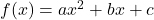
onde:
– 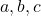 são números reais.
são números reais.
–  .
.
## Gráfico da Função Quadrática
O gráfico de uma função quadrática é uma **parábola**. O sentido da abertura da parábola depende do sinal de  :
:
– Se 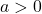 , a parábola se abre para cima.
, a parábola se abre para cima.
– Se 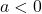 , a parábola se abre para baixo.
, a parábola se abre para baixo.
## Vértice da Parábola
O vértice da parábola é o ponto máximo ou mínimo da função, e suas coordenadas são dadas por:
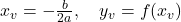
Portanto, as coordenadas do vértice são:
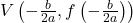
## Raízes da Função Quadrática
As raízes da função quadrática, também chamadas de zeros, são encontradas resolvendo-se a equação:
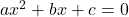
Utilizamos a **fórmula de Bhaskara** para encontrar as soluções:
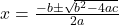
onde 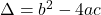 é o **discriminante** da equação. A partir do valor de
é o **discriminante** da equação. A partir do valor de  , temos:
, temos:
– Se 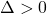 , existem duas raízes reais distintas.
, existem duas raízes reais distintas.
– Se 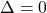 , existe uma raiz real dupla (ou duas raízes iguais).
, existe uma raiz real dupla (ou duas raízes iguais).
– Se 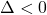 , não há raízes reais (as raízes são complexas).
, não há raízes reais (as raízes são complexas).
## Exemplo
Vamos analisar a função  .
.
### Passo 1: Identificar os coeficientes
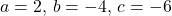
### Passo 2: Calcular o vértice
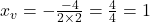
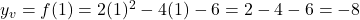
Portanto, o vértice é  .
.
### Passo 3: Calcular as raízes
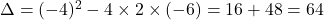
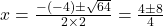
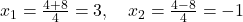
As raízes são  e
e  .
.
## Exercícios
1. Determine o vértice e as raízes da função quadrática 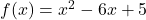 .
.
2. Para a função 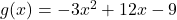 :
:
– (a) Determine o vértice.
– (b) Calcule as raízes.
3. A função 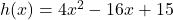 :
:
– (a) Encontre o vértice.
– (b) Verifique o número de raízes reais.
4. Considere a função 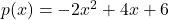 :
:
– (a) Determine o vértice.
– (b) Calcule o discriminante ( ) e identifique se há raízes reais.
) e identifique se há raízes reais.
## Respostas dos Exercícios
1. Para 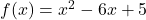 :
:
– Vértice: 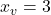 ,
,  →
→  .
.
– Raízes: 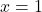 e
e 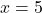 .
.
2. Para 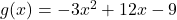 :
:
– Vértice: 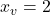 ,
,  →
→  .
.
– Raízes: 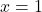 e
e  .
.
3. Para 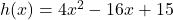 :
:
– Vértice: 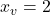 ,
,  →
→ 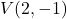 .
.
– Discriminante: 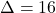 → Duas raízes reais:
→ Duas raízes reais:  e
e 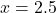 .
.
4. Para 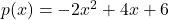 :
:
– Vértice: 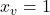 ,
, 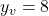 →
→ 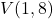 .
.
– Discriminante: 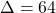 → Duas raízes reais:
→ Duas raízes reais:  e
e  .
.


