A função afim é um dos conceitos fundamentais da matemática, especialmente no estudo da álgebra. Ela é amplamente utilizada para descrever relações lineares entre variáveis. Vamos entender sua definição, propriedades, gráficos e exemplos práticos.
[affiliate_link id=’23’]
Definição
Uma função afim é uma função de primeiro grau que pode ser expressa na forma:
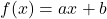
Onde:
 é o coeficiente angular (declive da reta).
é o coeficiente angular (declive da reta). é o coeficiente linear (intercepto com o eixo
é o coeficiente linear (intercepto com o eixo  ).
).
Como Identificar uma Função Afim
- Coeficiente Angular (
 ):
):
- Indica a inclinação da reta.
- Se
 , a reta é crescente.
, a reta é crescente.
- Se
 , a reta é decrescente.
, a reta é decrescente.
- Coeficiente Linear (
 ):
):
- Indica onde a reta intercepta o eixo
 .
.
- O ponto é dado por
 .
.
Gráfico da Função Afim
O gráfico de uma função afim é uma reta. Vamos entender como podemos desenhar essa reta:
- Encontrar o ponto de interseção com o eixo
 :
:  .
.
- Usar o coeficiente angular
 para determinar a inclinação da reta.
para determinar a inclinação da reta.
Exemplo 1: Vamos considerar a função:
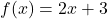
- Coeficiente angular
 (reta crescente).
(reta crescente).
- Coeficiente linear
 (intercepta o eixo
(intercepta o eixo  em
em  ).
).
Para esboçar o gráfico:
- Quando
 , temos
, temos  .
.
- Quando
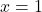 , temos
, temos  .
.
Portanto, os pontos  e
e  ajudam a desenhar a reta.
ajudam a desenhar a reta.
Gráfico do Exemplo 1
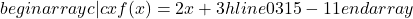
Outros Exemplos de Função Afim
Exemplo 2: Considere a função:
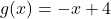
- Coeficiente angular
 (reta decrescente).
(reta decrescente).
- Coeficiente linear
 (intercepta o eixo
(intercepta o eixo  em
em  ).
).
Para traçar o gráfico:
- Quando
 , temos
, temos  .
.
- Quando
 , temos
, temos  .
.
Portanto, a reta passa pelos pontos  e
e  .
.
Exercícios de Fixação
Resolva os seguintes exercícios para praticar o conceito de função afim.
Exercício 1
Dada a função afim  :
:
- Determine o ponto de interseção com o eixo
 .
.
- Calcule o valor de
 .
.
- Esboce o gráfico.
Respostas:
- Interseção com o eixo
 .
.
 .
.- Pontos importantes para o gráfico:
 e
e  .
.
Exercício 2
Considere a função afim  :
:
- Identifique se a função é crescente ou decrescente.
- Encontre o valor de
 .
.
Respostas:
- A função é decrescente (
 ).
).
 .
.
Exercício 3
Qual é a função afim que passa pelos pontos  e
e  ?
?
Resposta:
- Coeficiente angular:
 .
.
- Função:
 .
.


