Notação Científica: Conceitos e Exercícios

A notação científica é uma maneira prática de representar números muito grandes ou muito pequenos, utilizando potências de base 10. Este método simplifica a escrita desses números, tornando-os mais fáceis de entender e manipular em cálculos matemáticos e científicos. Neste artigo, vamos explorar o conceito da notação científica e praticar com exercícios resolvidos passo a passo.

Conceito 1: O que é Notação Científica?

A notação científica consiste em expressar um número como o produto de dois fatores: um número decimal (chamado mantissa) entre 1 e 10, multiplicado por uma potência de 10. A forma geral é:

$a \times 10^n$

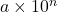
Onde:

$a$ é a mantissa, um número decimal tal que $1 \leq |a| < 10$ .
$n$ é o expoente, um número inteiro que indica quantas vezes a mantissa deve ser multiplicada por 10.

Exemplo: O número 350 pode ser escrito em notação científica como $3.5 \times 10^2$ .

Exercício 1: Escreva os seguintes números em notação científica.

4500
0.00078

Resolução Passo a Passo:

1. Converter 4500 para notação científica:

Para transformar 4500 em notação científica, devemos mover a vírgula decimal até obter um número entre 1 e 10. No caso de 4500, movemos a vírgula 3 casas para a esquerda, resultando em $4.5$ . Como movemos a vírgula 3 casas, o expoente será 3.

Resultado: $4.5 \times 10^3 <strong>2. Converter 0.00078 para notação científica:</strong> <div class="my-2"></div> Aqui, movemos a vírgula decimal para a direita até obter um número entre 1 e 10. Movemos a vírgula 4 casas para a direita, resultando em [latex] 7.8$ . Como movemos a vírgula para a direita, o expoente será negativo (-4).

Resultado: $7.8 \times 10^{-4} <div class="my-2"></div> <hr /> <h2>Conceito 2: Multiplicação de Números em Notação Científica</h2> Para multiplicar dois números na forma de notação científica, seguimos estas etapas: <ol start="1"> <li>Multiplique as mantissas.</li> <li>Some os expoentes das potências de 10.</li> <li>Ajuste o resultado, se necessário, para garantir que a mantissa esteja entre 1 e 10.</li> </ol> <div class="my-2"></div> Exemplo: Multiplique [latex] (2 \times 10^3) \times (3 \times 10^4)$ .

Exercício 2: Realize as seguintes multiplicações.

$(4 \times 10^5) \times (2 \times 10^3)$
$(6 \times 10^{-2}) \times (5 \times 10^{-4})$

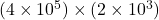
Resolução Passo a Passo:

1. Resolver 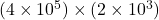$(4 \times 10^5) \times (2 \times 10^3)$ :

Passo 1: Multiplique as mantissas: $4 \times 2 = 8$ .

Passo 2: Some os expoentes: 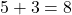$5 + 3 = 8$ .

Passo 3: Combine os resultados: $8 \times 10^8 Resultado: [latex] 8 \times 10^8$ .

2. Resolver $(6 \times 10^{-2}) \times (5 \times 10^{-4})$ :

Passo 1: Multiplique as mantissas: $6 \times 5 = 30$ .

Passo 2: Some os expoentes: $-2 + (-4) = -6$ .

Passo 3: Combine os resultados: $30 \times 10^{-6}$ .

Passo 4: Ajuste a mantissa para estar entre 1 e 10: Mova a vírgula 1 casa para a esquerda, alterando o expoente para -5.

Resultado final: $3 \times 10^{-5} <hr /> <h2>Conceito 3: Divisão de Números em Notação Científica</h2> Para dividir dois números na forma de notação científica, seguimos estas etapas: <ol start="1"> <li>Divida as mantissas.</li> <li>Subtraia os expoentes das potências de 10.</li> <li>Ajuste o resultado, se necessário, para garantir que a mantissa esteja entre 1 e 10.</li> </ol> <div class="my-2"></div> Exemplo: Divida [latex] (8 \times 10^6) \div (2 \times 10^3)$ .

Exercício 3: Realize as seguintes divisões.

$(12 \times 10^7) \div (3 \times 10^4)$
$(9 \times 10^{-3}) \div (3 \times 10^{-6})$

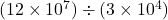
Resolução Passo a Passo:

1. Resolver 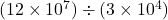$(12 \times 10^7) \div (3 \times 10^4)$ :

Passo 1: Divida as mantissas: $12 \div 3 = 4$ .

Passo 2: Subtraia os expoentes: $7 - 4 = 3$ .

Passo 3: Combine os resultados: $4 \times 10^3 Resultado: [latex] 4 \times 10^3$ .

2. Resolver $(9 \times 10^{-3}) \div (3 \times 10^{-6})$ :

Passo 1: Divida as mantissas: 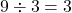$9 \div 3 = 3$ .

Passo 2: Subtraia os expoentes: $-3 - (-6) = 3$ .

Passo 3: Combine os resultados: $3 \times 10^3 Resultado: [latex] 3 \times 10^3$ .

Para somar ou subtrair números em notação científica, é necessário seguir algumas regras específicas. Primeiro, os números devem ter a mesma potência de 10, ou seja, a mesma ordem de grandeza

. Se os expoentes não forem iguais, você precisará ajustá-los para que sejam antes de realizar a operação

Aqui estão as etapas detalhadas:

Igualar os Expoentes : Se os expoentes dos números em notação científica são diferentes, deve-se ajustar um ou ambos os números de modo que eles tenham o mesmo expoente. Isso pode ser feito multiplicando ou dividindo o número decimal (mantissa) por uma potência de 10 adequada e ajustando o expoente consequentemente.
Somar ou Subtrair as Mantissas : Uma vez que os expoentes são iguais, você pode proceder a somar ou subtrair as mantissas como faria com números regulares.
Manter o Mesmo Expoente : Após realizar a soma ou subtração das mantissas, mantenha o mesmo expoente que foi igualado no primeiro passo.
Ajustar para Notação Científica Padrão : Por fim, verifique se o resultado está na forma padrão de notação científica, onde a mantissa deve estar entre 1 e 10. Se necessário, ajuste o resultado para atender a este critério.

Por exemplo, ao realizar a subtração $(4.1 \times 1 0^{-2}) - (2.6 \times 1 0^{-3})$ , primeiro igualamos os expoentes convertendo o segundo termo para $0.26 \times 1 0^{-2}$ . Depois disso, podemos subtrair as mantissas: $4.1 - 0.26 = 3.84$ , resultando em $3.84 \times 1 0^{-2}$

Essas são as principais regras e passos para realizar adições e subtrações em notação científica.

MatemáticaOpen

Ou verifique nossas categorias populares...

Contato

Editor Posts

A Evolução do Sistema Numeral na Matemática: Da Antiguidade aos Dias Atuais

A importancia da matemática

MatemáticaOpen

Ou verifique nossas categorias populares...

Notação Científica: Conceitos e Exercícios

Conceito 1: O que é Notação Científica?

Exercício 1: Escreva os seguintes números em notação científica.

Resolução Passo a Passo:

Exercício 2: Realize as seguintes multiplicações.

Resolução Passo a Passo:

Exercício 3: Realize as seguintes divisões.

Resolução Passo a Passo:

Matematicaopen

Postagens relacionadas

Números Racionais: Resolução de Problemas

Um Número Muito Famoso: O Triangular

Deixe um comentário Cancelar resposta

Você perdeu

Números Racionais: Resolução de Problemas

Notação Científica: Conceitos e Exercícios

Um Número Muito Famoso: O Triangular

Entendendo os Números Irracionais

Formas Fracionária e Decimal de um Número Racional

Arranjos na Matemática