Os números racionais são uma parte essencial da matemática e aparecem frequentemente em problemas do dia a dia. Eles são definidos como qualquer número que pode ser escrito na forma de fração $ \frac{a}{b} $, onde $ a $ e $ b $ são números inteiros e $ b \neq 0 $. Além disso, os números racionais podem ter representação decimal finita ou decimal periódica [[4]]. Vamos explorar o conceito de números racionais e resolver problemas envolvendo esses números, passo a passo.

—

Conceito 1: O que são números racionais?

Os números racionais incluem todos os números que podem ser escritos como frações, como $ \frac{1}{2} $, $ -\frac{3}{4} $, ou até mesmo números inteiros, já que qualquer inteiro $ n $ pode ser escrito como $ \frac{n}{1} $. Por exemplo:
– $ 5 = \frac{5}{1} $
– $ -3 = \frac{-3}{1} $

Além disso, números decimais finitos, como $ 0,25 $, também são racionais porque podem ser escritos como $ \frac{25}{100} $ ou simplificados para $ \frac{1}{4} $ [[8]].

Exercício 1
Escreva os seguintes números como frações:
1. $ 0,75 $
2. $ 2,5 $
3. $ -0,6 $

Resolução passo a passo:
1. Para $ 0,75 $, note que há duas casas decimais. Isso significa que podemos escrever $ 0,75 = \frac{75}{100} $. Simplificando por $ 25 $, temos:
.

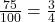2. Para $ 2,5 $, observe que há uma casa decimal. Escrevemos $ 2,5 = \frac{25}{10} $. Simplificando por $ 5 $, obtemos:
.

3. Para $ -0,6 $, escrevemos $ -0,6 = \frac{-6}{10} $. Simplificando por $ 2 $, temos:
.

—

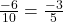Conceito 2: Adição e subtração de números racionais

Para somar ou subtrair números racionais, é necessário que eles tenham o mesmo denominador. Se os denominadores forem diferentes, devemos encontrar o mínimo múltiplo comum (MMC) entre eles antes de realizar a operação [[6]].

Exercício 2
Resolva as seguintes operações:
1. $ \frac{1}{4} + \frac{3}{8} $
2. $ \frac{5}{6} – \frac{1}{3} $

Resolução passo a passo:
1. Para $ \frac{1}{4} + \frac{3}{8} $, o MMC entre $ 4 $ e $ 8 $ é $ 8 $. Reescrevemos as frações com denominador $ 8 $:
.
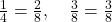Agora somamos:
.

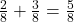2. Para $ \frac{5}{6} – \frac{1}{3} $, o MMC entre $ 6 $ e $ 3 $ é $ 6 $. Reescrevemos as frações com denominador $ 6 $:
.
Agora subtraímos:
.

—

Conceito 3: Multiplicação de números racionais

A multiplicação de números racionais é feita multiplicando-se os numeradores entre si e os denominadores entre si. Não é necessário que os denominadores sejam iguais [[6]].

Exercício 3
Calcule o produto das seguintes frações:
1. $ \frac{2}{3} \times \frac{4}{5} $
2. $ \frac{-3}{7} \times \frac{2}{9} $

**Resolução passo a passo:**
1. Para $ \frac{2}{3} \times \frac{4}{5} $, multiplicamos os numeradores e os denominadores:
.

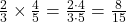2. Para $ \frac{-3}{7} \times \frac{2}{9} $, multiplicamos os numeradores e os denominadores. Note que o sinal será negativo porque um dos fatores é negativo:
.

—

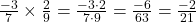Conceito 4: Divisão de números racionais

Para dividir números racionais, multiplicamos a primeira fração pelo inverso da segunda fração. O inverso de uma fração $ \frac{a}{b} $ é $ \frac{b}{a} $ [[6]].

Exercício 4
Resolva as seguintes divisões:
1. $ \frac{3}{4} \div \frac{2}{5} $
2. $ \frac{-1}{2} \div \frac{3}{8} $

Resolução passo a passo:
1. Para $ \frac{3}{4} \div \frac{2}{5} $, multiplicamos $ \frac{3}{4} $ pelo inverso de $ \frac{2}{5} $, que é $ \frac{5}{2} $:
.

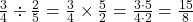2. Para $ \frac{-1}{2} \div \frac{3}{8} $, multiplicamos $ \frac{-1}{2} $ pelo inverso de $ \frac{3}{8} $, que é $ \frac{8}{3} $:
.

—

Conclusão

Os números racionais são fundamentais para resolver problemas matemáticos e cotidianos. Ao dominar as operações básicas (adição, subtração, multiplicação e divisão), você estará preparado para enfrentar desafios mais complexos. Pratique os exercícios acima e explore mais exemplos para consolidar seu aprendizado!