A permutação é um dos conceitos mais importantes da matemática combinatória. Ela nos ajuda a calcular o número de maneiras diferentes que podemos organizar elementos em uma ordem específica. Neste artigo, vamos explorar dois tipos principais de permutações: permutação simples e permutação com repetição , além de fornecer exercícios resolvidos passo a passo.

---

O que é Permutação Simples?

A permutação simples ocorre quando todos os elementos de um conjunto são distintos (não há repetição). Nesse caso, queremos determinar quantas formas diferentes podemos ordenar esses elementos

Fórmula da Permutação Simples

Se temos $n$ elementos distintos, o número total de permutações possíveis é dado por:

Pn​=n!

Onde:

• $n!$ (lê-se “n fatorial”) é o produto de todos os números inteiros positivos de 1 até $n$.
• Por exemplo, $4!=4\times 3\times 2\times 1=24$.

Em notação :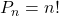

---

Exemplo Resolvido: Permutação Simples

Problema: Quantas formas diferentes podemos organizar as letras da palavra “MATE”?

Resolução Passo a Passo:

1. Identifique o número de elementos distintos: A palavra “MATE” possui 4 letras distintas ($M,A,T,E$).
2. Use a fórmula da permutação simples:P4​=4!=4×3×2×1=24
3. Conclusão: Existem 24 formas diferentes de organizar as letras da palavra “MATE”.

---

O que é Permutação com Repetição?

A permutação com repetição ocorre quando alguns elementos do conjunto se repetem. Nesse caso, devemos dividir o fatorial do número total de elementos pelos fatoriais das repetições para eliminar contagens duplicadas

Fórmula da Permutação com Repetição

Se temos $n$ elementos no total, onde alguns elementos se repetem k1​,k2​,…,km​ vezes, o número total de permutações é dado por:

Pn(k1​,k2​,…,km​)​=k1​!⋅k2​!⋅…⋅km​!n!​

Em notação :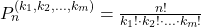

---

Exemplo Resolvido: Permutação com Repetição

Problema: Quantas formas diferentes podemos organizar as letras da palavra “BANANA”?

Resolução Passo a Passo:

1. Identifique o número total de elementos: A palavra “BANANA” possui 6 letras no total.
2. Determine as repetições:
   • A letra $A$ aparece 3 vezes.
   • A letra $N$ aparece 2 vezes.
   • A letra $B$ aparece 1 vez.
3. Use a fórmula da permutação com repetição:P6(3,2,1)​=3!⋅2!⋅1!6!​
4. Calcule os fatoriais:
   • $6!=6\times 5\times 4\times 3\times 2\times 1=720$
   • $3!=3\times 2\times 1=6$
   • $2!=2\times 1=2$
   • $1!=1$
5. Substitua na fórmula:P6(3,2,1)​=6⋅2⋅1720​=12720​=60
6. Conclusão: Existem 60 formas diferentes de organizar as letras da palavra “BANANA”.

---

Exercícios Propostos

1. Permutação Simples: Quantas formas diferentes podemos organizar as letras da palavra “CASA”?
   Dica: Considere que todas as letras são distintas.
2. Permutação com Repetição: Quantas formas diferentes podemos organizar as letras da palavra “MISSISSIPPI”?
   Dica: Identifique as repetições das letras $I,S,$ e $P$.

---

Respostas dos Exercícios

1. Permutação Simples:
   • Total de letras: 4 ($C,A,S,A$).
   • Como todas as letras são distintas, usamos P4​=4!.
   • Resposta: $4!=24$ formas.
2. Permutação com Repetição:
   • Total de letras: 11.
   • Repetições: $I$ (4 vezes), $S$ (4 vezes), $P$ (2 vezes).
   • Use a fórmula:P11(4,4,2)​=4!⋅4!⋅2!11!​
   • Calcule:
     • $11!=39916800$
     • $4!=24$
     • $2!=2$
     • Substitua:P11(4,4,2)​=24⋅24⋅239916800​=115239916800​=34650
   • Resposta: $34650$ formas.

---

Esperamos que este guia tenha ajudado você a entender melhor os conceitos de permutação simples e permutação com repetição . Pratique os exercícios propostos para consolidar seu aprendizado! 😊