Observe como podemos traçar uma circunferência circunscrita a um pentágono regular.

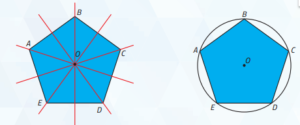
1a) Traçamos a mediatriz de cada lado do                         
pentágono regular, obtendo um ponto O
na interseção dessas mediatrizes.
Dizemos que O é o centro do polígono.

2a) Com centro em O, traçamos uma
circunferência contendo todos os vértices
do pentágono regular, ou seja, que
circunscreve esse polígono.

Ao traçarmos segmentos de reta com uma extremidade em O e
a outra em cada vértice do pentágono regular, obtemos cinco triângulos, conforme mostrado ao lado.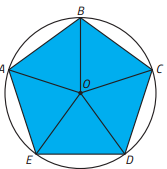Note que, em cada um desses triângulos, um dos lados corresponde ao lado do pentágono
regular, e os outros dois lados, a raios da mesma circunferência. Portanto, podemos afirmar
que esses triângulos são isósceles e congruentes (caso LLL de congruência de triângulos).
De maneira análoga, é possível most rar que todo polígono regular de n lados pode ser decom￾posto, a partir de seu centro, em n triângulos isósceles congruentes.
Agora, considere esse mesmo pentágono regular decomposto da maneira apresentada.
Denominamos apótema do pentágono o segmento de reta com extremidades em O e no ponto
médio de um lado desse polígono regular. O apótema é perpendicular ao lado do polígono
regula.

» Nesse caso, a é o apótema
do pentágono regular
ABCDE. A medida do
apótema corresponde à
altura dos triângulos em
que o pentágono regular
foi decomposto.

 

 

Exercícios:

5 Questões sobre Polígonos Regulares com Solução Passo a Passo

1. Qual é a medida de cada ângulo interno de um hexágono regular?

Solução:

• Um hexágono regular possui 6 lados iguais e 6 ângulos internos iguais.

[affiliate_link id=’20’]

• A soma dos ângulos internos de um polígono de n lados é dada por (n-2) * 180°.
• Para um hexágono (n = 6), a soma dos ângulos internos é (6-2) * 180° = 720°.
• Como os ângulos internos são iguais, cada ângulo mede 720° / 6 = 120°.

Resposta: Cada ângulo interno de um hexágono regular mede 120°.

2. Um octógono regular tem lado medindo 5 cm. Qual é o perímetro desse octógono?

Solução:

• Um octógono possui 8 lados.
• Se cada lado mede 5 cm, então o perímetro (soma dos lados) é 8 * 5 cm = 40 cm.

Resposta: O perímetro do octógono é 40 cm.

3. Quantos lados tem um polígono regular cujo ângulo externo mede 45°?

Solução:

• A soma dos ângulos externos de qualquer polígono é sempre 360°.
• Se cada ângulo externo mede 45°, então o número de lados é 360° / 45° = 8.

Resposta: O polígono tem 8 lados (é um octógono).

4. Um pentágono regular está inscrito em uma circunferência de raio 6 cm. Qual é a medida do apótema desse pentágono?

• Observação: Essa questão requer conhecimentos de trigonometria e não pode ser resolvida apenas com as fórmulas básicas de polígonos regulares.
• Sugestão: Para resolver essa questão, é necessário dividir o pentágono em 5 triângulos isósceles congruentes, onde o raio da circunferência é a hipotenusa de cada triângulo e o apótema é a altura. Utilizando trigonometria, podemos encontrar o valor do apótema.

5. Um quadrado tem área igual a 64 cm². Qual é a medida de sua diagonal?

Solução:

• Se a área do quadrado é 64 cm², então o lado do quadrado mede √64 cm = 8 cm.
• A diagonal de um quadrado divide-o em dois triângulos retângulos isósceles.
• Aplicando o Teorema de Pitágoras, temos: diagonal² = lado² + lado²
• diagonal² = 8² + 8² = 128
• diagonal = √128 ≈ 11,31 cm

Resposta: A medida da diagonal do quadrado é aproximadamente 11,31 cm.

[affiliate_link id=’14’]