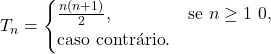Os números triangulares são uma sequência de números que têm uma propriedade única: eles podem ser representados geometricamente em forma de triângulos equiláteros. Esses números aparecem frequentemente na matemática e possuem conexões com outras áreas do conhecimento, como a geometria e a programação.
Conceito: O Que São Números Triangulares?
Um número triangular é definido como a soma dos primeiros n números naturais. Por exemplo, o primeiro número triangular é 1 (representado por uma bolinha), o segundo é 3 (três bolinhas formando um triângulo), o terceiro é 6, e assim por diante
A fórmula geral para calcular o n-ésimo número triangular é:
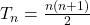
Exercício 1: Encontre o 5º Número Triangular
Pergunta: Qual é o quinto número triangular?
Resolução Passo a Passo:
Para encontrar o quinto número triangular (T5), substituímos n=5 na fórmula:
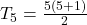
Primeiro, calculamos dentro dos parênteses:
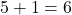
Então multiplicamos:
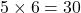
Finalmente, dividimos por 2:
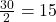
Resposta: O quinto número triangular é  .
.
Conceito: A Relação Entre Números Triangulares e Outros Números
Os números triangulares estão intimamente relacionados com outros tipos de sequências numéricas, como os números quadrados e os números hexagonais. Além disso, eles também aparecem na combinação binomial, onde cada número triangular pode ser expresso como:
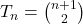
Isso significa que o n-ésimo número triangular é igual ao número de maneiras de escolher 2 itens de n+1 itens.
Exercício 2: Relacione os Números Triangulares com Combinações
Pergunta: Mostre que o terceiro número triangular (T3) pode ser calculado usando combinações.
Resolução Passo a Passo:
O terceiro número triangular (T3) deve ser igual a:

Agora, usamos a fórmula para combinações:
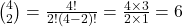
Resposta: O terceiro número triangular é  , o que confirma nossa relação com as combinações.
, o que confirma nossa relação com as combinações.
Conceito: Sequências Numéricas e Programação
Além de sua importância teórica, os números triangulares também são úteis na prática, especialmente em programação. Em linguagens como Python, podemos criar programas simples para gerar esses números.
Por exemplo, aqui está um programa básico em Python para gerar os primeiros números triangulares:
Este código gera os primeiros 10 números triangulares
Exercício 3: Implemente a Função em LaTeX
Pergunta: Escreva a função acima em notação matemática usando LaTeX.
Resolução Passo a Passo:
Podemos escrever a função de números triangulares em LaTeX da seguinte forma:
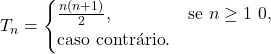
Resposta: A função dos números triangulares escrita em LaTeX é:
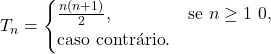
Conclusão
Os números triangulares são mais do que apenas uma curiosidade matemática; eles desempenham papéis fundamentais em várias áreas do conhecimento. Ao entender sua definição e explorar exemplos práticos, você pode desenvolver uma apreciação mais profunda por essa sequência fascinante. Pratique os exercícios acima e veja como eles se conectam à programação e à combinatoria!