Os triângulos são figuras geométricas fundamentais que aparecem em diversas situações do dia a dia. Eles são usados para resolver problemas práticos em áreas como construção civil, navegação, design gráfico, astronomia e até mesmo em atividades cotidianas simples. Nesta seção, vamos explorar como os conceitos de triângulos podem ser aplicados em problemas reais, com exemplos concretos e resoluções passo a passo.

---

Aplicação 1: Medindo Alturas Inacessíveis

Conceito:

Quando queremos medir a altura de algo inacessível, como um prédio ou uma árvore, podemos usar o conceito de triângulo retângulo e a trigonometria . A trigonometria nos permite relacionar ângulos e lados de um triângulo.

A relação mais comum é dada pelo seno, cosseno e tangente:

• Tangente: tan(θ)=cateto adjacentecateto oposto​

Problema Prático:

Você está a $30\text{m}$ de distância de um prédio e mede o ângulo de elevação até o topo do prédio como 45∘. Qual é a altura do prédio?

Resolução Passo a Passo:

1. Identifique os elementos do problema:
   • Distância até o prédio ($\text{cateto adjacente}$): $30\text{m}$
   • Ângulo de elevação ($\theta$): 45∘
   • Altura do prédio ($\text{cateto oposto}$): desconhecida.
2. Use a fórmula da tangente:
3. Sabemos que tan(45∘)=1, então:
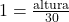
4. Resolva para a altura:

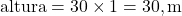
Resposta: A altura do prédio é $30\text{m}$.

---

Aplicação 2: Construção de Rampas

Conceito:

Na construção civil, rampas precisam ter inclinações específicas para garantir acessibilidade e segurança. A inclinação de uma rampa pode ser determinada usando a relação entre a altura (subida) e o comprimento horizontal (extensão).

Essa relação pode ser representada por: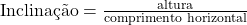

Problema Prático:

Uma rampa precisa ter uma inclinação máxima de $10\%$ (ou seja, subir $1\text{m}$ para cada $10\text{m}$ de extensão horizontal). Se a altura da rampa for $1,5\text{m}$, qual deve ser o comprimento horizontal mínimo?

Resolução Passo a Passo:

1. Use a fórmula da inclinação:
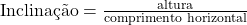
2. Substitua os valores conhecidos:
3. Resolva para o comprimento horizontal:

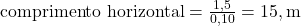
Resposta: O comprimento horizontal mínimo deve ser $15\text{m}$.

---

Aplicação 3: Divisão de Terrenos

Conceito:

Ao dividir um terreno triangular em partes iguais, podemos usar o conceito de área de um triângulo . A área de um triângulo é dada por:

Problema Prático:

Um terreno triangular tem base de $20\text{m}$ e altura de $15\text{m}$. Ele precisa ser dividido em dois lotes com áreas iguais. Qual deve ser a altura de cada lote?

Resolução Passo a Passo:

1. Calcule a área total do terreno:
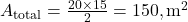
2. Cada lote deve ter metade dessa área:
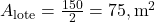
3. Para manter a mesma base ($20\text{m}$), calcule a nova altura: 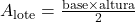Substitua os valores:
4. Resolva para a altura:

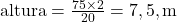
Resposta: Cada lote deve ter uma altura de $7,5\text{m}$.

---

Aplicação 4: Triângulos na Navegação

Conceito:

Na navegação, os triângulos são usados para calcular distâncias e direções. Por exemplo, ao navegar em um barco, podemos usar o Teorema de Pitágoras para calcular a distância entre dois pontos no mapa.

Problema Prático:

Um barco navega $6\text{km}$ para o leste e depois $8\text{km}$ para o norte. Qual é a distância direta do ponto inicial ao ponto final?

Resolução Passo a Passo:

1. Represente o problema como um triângulo retângulo:
   • Cateto leste: $6\text{km}$
   • Cateto norte: $8\text{km}$
   • Hipotenusa (distância direta): desconhecida.
2. Use o Teorema de Pitágoras: Substitua os valores:
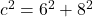
3. Calcule os quadrados:
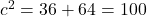
4. Extraia a raiz quadrada:

Resposta: A distância direta é $10\text{km}$.

---

Conclusão

Os triângulos são ferramentas poderosas para resolver problemas do dia a dia. Desde medir alturas inacessíveis até planejar construções e navegações, os conceitos matemáticos envolvendo triângulos são amplamente aplicáveis. Com prática e compreensão dos princípios básicos, você poderá resolver problemas reais de forma eficiente e precisa.