Os triângulos são figuras geométricas fundamentais na matemática. Eles possuem três lados, três ângulos internos e sempre são convexos . Neste artigo, vamos explorar os conceitos básicos sobre triângulos, seguidos de exercícios práticos com resoluções passo a passo. Além disso, utilizaremos notações matemáticas em para facilitar a compreensão.

Conceito 1: O que é um triângulo?
Um triângulo é um polígono formado por três segmentos de reta que se conectam em três vértices. A soma dos ângulos internos de qualquer triângulo é sempre igual a 180∘.

Em notação matemática, podemos representar isso como:

Exercício 1:
Considere um triângulo cujos dois ângulos medem 50∘
e 60∘.

Qual é a medida do terceiro ângulo?

Resolução Passo a Passo:
Sabemos que a soma dos ângulos internos de um triângulo é 180∘.
Representamos o terceiro ângulo como x.
Montamos a equação:

Simplificamos:

Isolamos x:

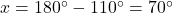
Resposta: O terceiro ângulo mede 70∘.

Conceito 2: Classificação dos Triângulos
Os triângulos podem ser classificados de acordo com seus lados ou ângulos:

Quanto aos lados:
Equilátero : Todos os lados têm a mesma medida.
Isósceles : Dois lados têm a mesma medida.
Escaleno : Todos os lados têm medidas diferentes.
Quanto aos ângulos:
Acutângulo : Todos os ângulos são menores que 90∘.
Retângulo : Possui um ângulo reto (90∘).
Obtusângulo : Possui um ângulo maior que 90∘.
Exercício 2:
Determine a classificação do triângulo cujos lados medem 5cm, 5cm e 8cm.

Resolução Passo a Passo:
Observamos que dois lados têm a mesma medida (5cm).
Concluímos que o triângulo é isósceles porque possui dois lados iguais.
Resposta: O triângulo é isósceles.

Conceito 3: Área de um Triângulo
A área de um triângulo pode ser calculada usando a fórmula:

Onde “base” é um dos lados do triângulo e “altura” é a distância perpendicular desse lado até o vértice oposto .

Exercício 3:
Calcule a área de um triângulo cuja base mede 10cm e a altura mede 6cm.

Resolução Passo a Passo:
Substituímos os valores na fórmula:

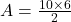
Realizamos a multiplicação:

Calculamos o resultado:

Resposta: A área do triângulo é 30cm.

Conceito 4: Semelhança de Triângulos
Dois triângulos são semelhantes quando seus ângulos correspondentes são congruentes e seus lados são proporcionais. A proporção entre os lados pode ser escrita como:

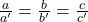
Exercício 4:
Dois triângulos são semelhantes. O primeiro tem lados medindo 3cm, 4cm e 5cm. O segundo triângulo tem um lado correspondente ao lado de 4cm medindo 8cm. Determine os outros dois lados do segundo triângulo.

Resolução Passo a Passo:
A razão de semelhança entre os lados é:

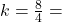
Multiplicamos os outros lados do primeiro triângulo pela razão k:
Lado correspondente a 3cm:

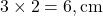
Lado correspondente a 5cm:

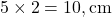
Resposta: Os lados do segundo triângulo medem 6cm, 8cm e 10cm.

Conceito 5: Teorema de Pitágoras (Triângulo Retângulo)
Em um triângulo retângulo, o quadrado da hipotenusa (c) é igual à soma dos quadrados dos catetos (a e b):

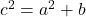
Exercício 5:
Determine a medida da hipotenusa de um triângulo retângulo cujos catetos medem 6cm e 8cm.

Resolução Passo a Passo:
Aplicamos o Teorema de Pitágoras:

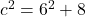
Calculamos os quadrados:

Somamos:

Extraímos a raiz quadrada:

Resposta: A hipotenusa mede 10cm.

Com esses conceitos e exercícios, você já está preparado para entender melhor os triângulos e resolver problemas relacionados a eles. Continue praticando e aprofundando seus conhecimentos!