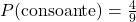1) Princípio Multiplicativo
Enunciado:
O Sr. Carlos tem uma lanchonete e oferece 5 tipos de pães, 3 tipos de recheios e 6 tipos de molhos. Ele utilizou o princípio multiplicativo para descobrir de quantas maneiras diferentes um cliente pode montar seu sanduíche escolhendo um item de cada categoria.
Qual foi o valor encontrado pelo Sr. Carlos?
Fórmula:
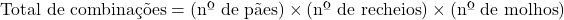
Cálculo:
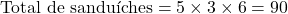
Resposta: O Sr. Carlos pode montar 90 sanduíches diferentes.
2) Simplificação de Fatoriais
Enunciado:
Simplifique as seguintes expressões fatoriais.
a) 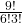
b) 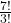
c) 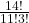
Fórmula:
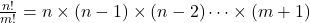
Cálculos:
a)
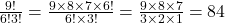
b)
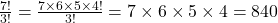
c)
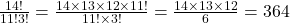
3) Anagramas com Letras Repetidas
Enunciado:
Quantos anagramas diferentes podem ser formados com a palavra “TATATA”?
Fórmula:
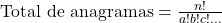
Cálculo:
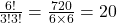
Resposta: 20 anagramas.
4) Permutação com Repetição
Enunciado:
Quantos números diferentes de 5 algarismos podem ser formados usando os dígitos 1, 2, 2, 3, 4 (sem deixar nenhum de fora)?
Fórmula:
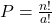
Cálculo:
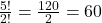
Resposta: 60 números diferentes.
5) Arranjo Simples
Enunciado:
Considerando uma equipe de 8 atletas, precisa-se escolher 3 deles para formar um trio de revezamento.
De quantas maneiras diferentes esse trio pode ser escolhido, considerando que a ordem dos atletas no trio importa?
Fórmula:
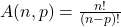
Cálculo:
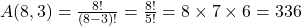
Resposta: 336 maneiras diferentes.
6) Arranjo Simples com Algarismos Distintos
Enunciado:
Quantos números de três algarismos distintos podem ser formados utilizando os dígitos 4, 5, 6, 7, 8 e 9?
Fórmula:
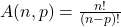
Cálculo:
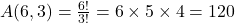
Resposta: 120 números diferentes.
7) Combinação Simples
Enunciado:
Um torneio de dominó está sendo organizado com 12 participantes. Se forem selecionados 4 participantes para um jogo em equipe, de quantas maneiras diferentes os participantes podem ser escolhidos para formar uma equipe?
Fórmula:
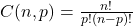
Cálculo:
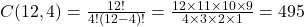
Resposta: 495 maneiras diferentes.
8) Probabilidade com Espaço Amostral
Enunciado:
As letras da palavra GEOMETRIA são escritas em cartões e colocadas em uma caixa.
Um cartão é sorteado ao acaso.
a) Qual é o espaço amostral?
b) Qual a probabilidade de sair a letra “E”?
c) Qual a probabilidade de sair uma consoante?
Fórmula:
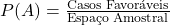
Cálculos:
a) Espaço amostral: 9
b)
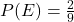
c)