Grandezas proporcionais fazem parte de situações do cotidiano, desde calcular custos de compras até estimar o tempo de viagens. Este artigo vai explicar de forma simples e visual o conceito de grandezas diretamente proporcionais e grandezas inversamente proporcionais, com exemplos práticos, gráficos e exercícios.

---

1. Grandezas Diretamente Proporcionais

Duas grandezas são diretamente proporcionais quando, ao aumentar uma delas, a outra também aumenta na mesma proporção. Da mesma forma, ao diminuir uma, a outra também diminui proporcionalmente.

Fórmula Geral

Camera Jgl P11 Wifi Segurança 6 Mp 4k Lente Dupla Zoom Vigilância Cor Preto Comprar

Se $x$ e $y$ são grandezas diretamente proporcionais: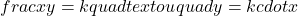
Onde $k$ é a constante de proporcionalidade.

---

Exemplo 1: Consumo de combustível

Um carro consome 10 litros de combustível para percorrer 200 km. O consumo é diretamente proporcional à distância. Se quisermos saber quantos litros serão necessários para percorrer 500 km:

---

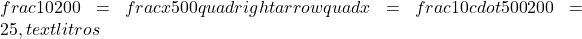
Gráfico de Proporcionalidade Direta

No caso das grandezas diretamente proporcionais, o gráfico é uma linha reta que passa pela origem (0,0).

Exemplo Visual:

Para o exemplo do consumo de combustível:

• Distância ($x$): 0, 100, 200, 300, 500 km
• Combustível ($y$): 0, 5, 10, 15, 25 litros

O gráfico representará esses valores.

---

2. Grandezas Inversamente Proporcionais

Duas grandezas são inversamente proporcionais quando, ao aumentar uma delas, a outra diminui proporcionalmente, e o produto das grandezas é sempre constante.

Fórmula Geral

Se $x$ e $y$ são grandezas inversamente proporcionais: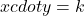
Onde $k$ é a constante de proporcionalidade.

---

Exemplo 2: Tempo e velocidade

Um carro leva 4 horas para percorrer 240 km a uma velocidade de 60 km/h. Se aumentarmos a velocidade para 80 km/h, o tempo diminuirá:

---

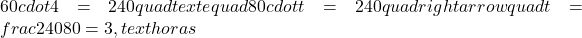
Gráfico de Proporcionalidade Inversa

No caso das grandezas inversamente proporcionais, o gráfico é uma hipérbole.

Exemplo Visual:

Para o exemplo de velocidade e tempo:

• Velocidade ($x$): 40, 60, 80, 120 km/h
• Tempo ($y$): 6, 4, 3, 2 horas

O gráfico mostrará a relação.

---

3. Comparação entre os Gráficos

Diretamente Proporcionais

O gráfico é sempre uma linha reta com inclinação positiva. Quanto maior o valor de $x$, maior será o valor de $y$.

Inversamente Proporcionais

O gráfico é uma curva decrescente, onde os valores de $y$ diminuem conforme $x$ aumenta.

---

4. Exercícios para Fixação

Exercício 1: Proporção Direta

Um caminhão consome 15 litros de combustível para percorrer 180 km. Quantos litros serão necessários para percorrer 300 km?

Resposta: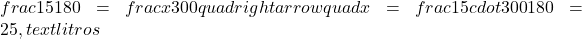

---

Exercício 2: Proporção Inversa

Seis pedreiros levam 10 dias para construir um muro. Quantos dias levariam 15 pedreiros para construir o mesmo muro?

Resposta: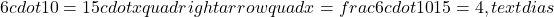

---

Exercício 3: Gráfico de Proporcionalidade Direta

Construa o gráfico da relação entre os valores de $x=\{0,2,4,6\}$ e $y=\{0,10,20,30\}$, sabendo que $y=5x$.

---

Exercício 4: Gráfico de Proporcionalidade Inversa

Um carro percorre 240 km. Sabendo que a relação é inversamente proporcional, construa o gráfico da relação entre as velocidades $x=\{40,60,80,120\}$ e os tempos correspondentes y=240xy = frac{240}{x}y=x240​.

---