Os arranjos simples são um conceito fundamental na Combinatória, uma área da Matemática que estuda as diferentes formas de agrupar ou organizar elementos. Neste artigo, vamos explorar o que são os arranjos simples, suas propriedades, exemplos explicativos e exercícios resolvidos para consolidar o aprendizado.
O que são Arranjos Simples?
Os arranjos simples são agrupamentos ordenados de elementos retirados de um conjunto maior. Diferentemente das combinações, nos arranjos, a ordem dos elementos é importante.
Matematicamente, o número de arranjos simples de nn elementos tomados pp a pp é dado por:
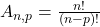
Definição de Termos:
- nn: total de elementos do conjunto.
- pp: número de elementos escolhidos para o arranjo.
- !!: fatorial, ou seja, o produto de todos os inteiros positivos até o número dado.
Propriedades dos Arranjos Simples
- Ordem Importa: A ordem dos elementos no arranjo faz diferença. Por exemplo, os arranjos (A, B) e (B, A) são considerados diferentes.
- Fatorial na Fórmula: O uso de fatoriais na fórmula reflete todas as permutações possíveis dos elementos.
- p≤np \leq n: Não é possível selecionar mais elementos do que existem no conjunto original.
- Crescimento Exponencial: Conforme nn aumenta, o número de arranjos cresce rapidamente devido ao uso de fatoriais.
Exemplos Explicativos
Exemplo 1: Arranjo de 3 letras retiradas de um conjunto de 5 letras
Considere o conjunto {A,B,C,D,E}\{A, B, C, D, E\}. Queremos formar arranjos de 3 letras.
A fórmula é aplicada como segue:
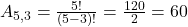
Assim, existem 60 arranjos diferentes. Alguns exemplos de arranjos são:
- ABC, ACB, BAC, BCA, CAB, CBA, etc.
Exemplo 2: Organização de 4 pessoas em 2 cadeiras
Suponha que temos 4 pessoas: Ana (A), Bruno (B), Carla (C) e Diego (D). Quantas formas diferentes existem de organizar 2 pessoas em cadeiras?
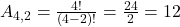
As organizações são:
- AB, BA, AC, CA, AD, DA, BC, CB, BD, DB, CD, DC.
Representação Gráfica
Imagine um gráfico de árvore onde cada ramo representa uma escolha de elemento. Para A3,2A_{3,2}:
- No primeiro nível, escolha entre A, B, ou C.
- No segundo nível, escolha entre os dois elementos restantes. O total de caminhos corresponde ao número de arranjos.
Essa representação visual ajuda a entender a sequência de escolhas e o motivo pelo qual a ordem importa.
Exercícios Resolvidos
- Quantos arranjos podem ser formados com 4 alunos escolhidos de uma turma de 6?
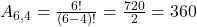
- De um baralho de 52 cartas, quantas sequências de 5 cartas podem ser formadas?
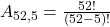
Devido ao tamanho dos cálculos, é prático usar calculadoras ou softwares matemáticos.
Proposta de Exercícios
- De quantas maneiras diferentes podemos formar arranjos de 2 letras a partir do conjunto {X,Y,Z,W}\{X, Y, Z, W\}?
- Quantas maneiras existem de organizar 3 jogadores em 3 posições diferentes a partir de um grupo de 5 jogadores?
- Um professor quer organizar 4 alunos em uma fila. De quantas maneiras isso pode ser feito?
Respostas em LaTeX:
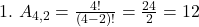
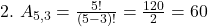
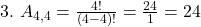
Este artigo buscou trazer clareza ao tema de arranjos simples, utilizando explicações acessíveis e exemplos detalhados. Para se aprofundar, pratique os exercícios propostos e experimente criar situações reais que envolvam arranjos!